DFS & BFS 란?
먼저 읽으면 좋은 글: [Python] 그래프 (인접 행렬, 인접 리스트) + DFS/BFS를 배우기 앞서 알아야 할 개념들 (탐색 알고리즘, 자료구조)
위에 글에서도 언급했듯, DFS(Depth1-First Search)와 BFS(Breadth2-First Search)는 그래프 탐색 알고리즘(Graph traversal algorithm)이다. 그래프 탐색 알고리즘이란, 그래프의 모든 꼭짓점(Node 또는 Vertex라 한다)을 방문하는 알고리즘을 의미한다.
DFS vs BFS

DFS와 BFS의 차이점은 바로 노드 방문 순서이다.
DFS
DFS는 깊이 우선 탐색이라는 그 이름답게 그래프의 깊은 부분을 우선적으로 탐색하는 알고리즘이다. 스택 자료구조를 사용하여 그래프의 가장 깊은 곳까지 방문한 뒤, 다시 돌아가 다른 경로를 탐색한다.
구체적인 동작 과정:
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리. (이미 방문(탐색)했던 노드를 재방문하지 않기 위해)
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있다면 그 노드를 스택에 넣고 방문 처리. 만약 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼냄.
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복.
만약 아래와 같은 그래프가 있고 이걸 DFS로 탐색해야 한다고 하자.

상세한 동작 과정 풀이:
1. 시작 노드인 1을 스택에 삽입하고 방문 처리한다.
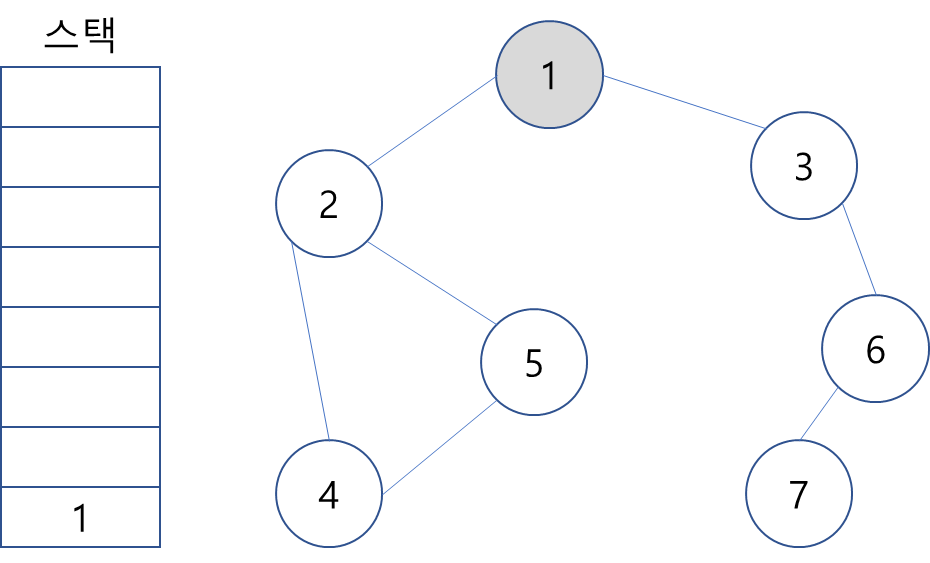
2. 스택 최상단 노드인 1에게는 인접하지만 방문하지 않은 노드 2와 3이 있다. 이 중에 가장 작은 노드인 2를 스택에 넣고 방문 처리. (일반적으로 인접한 노드 중에서 방문하지 않은 노드가 여러 개 있다면 번호가 낮은 순부터 처리한다.)
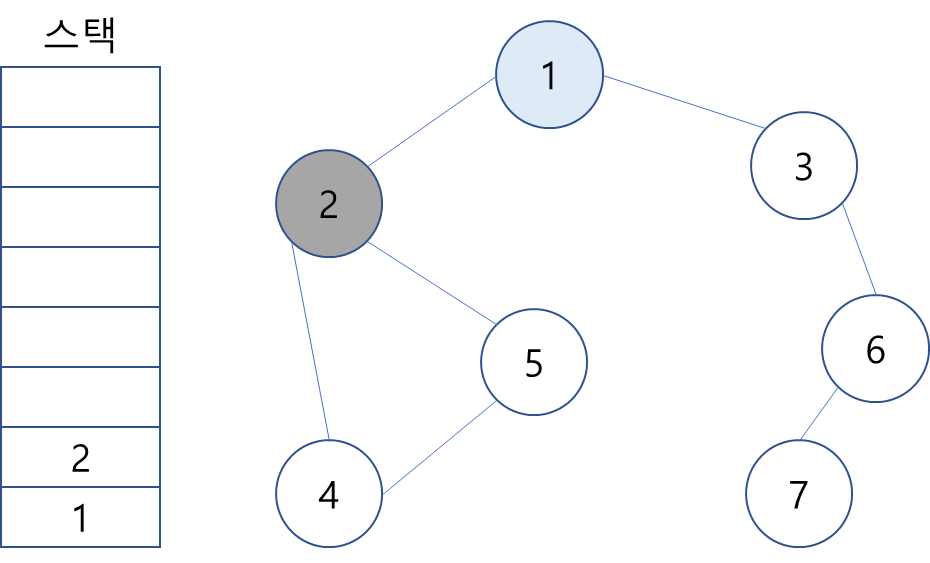
3. 스택의 최상단 노드인 2에 방문하지 않은 인접 노드 4와 5 중 가장 작은 4를 스택에 넣고 방문 처리.
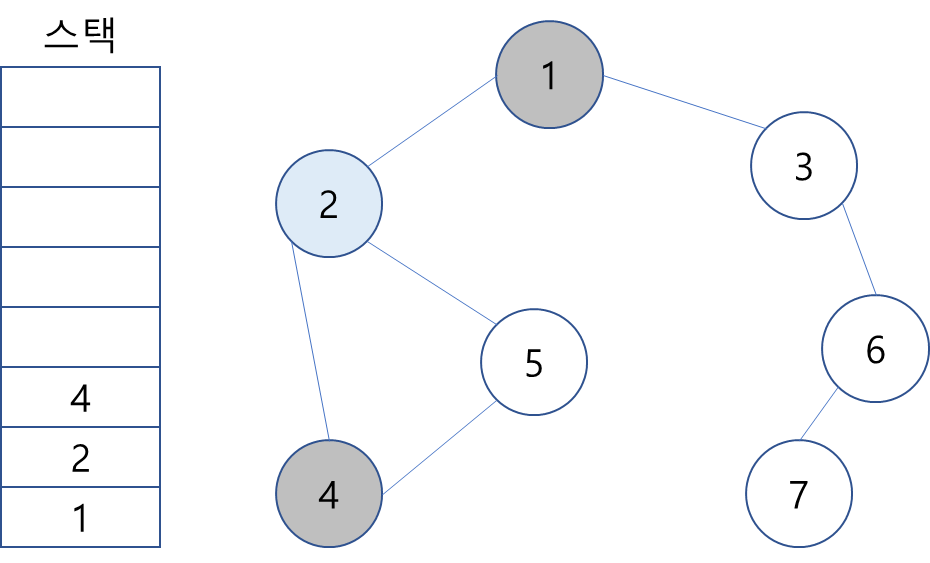
4. 스택 최상단 노드인 4에 방문하지 않은 인접 노드 5를 스택에 넣고 방문 처리.
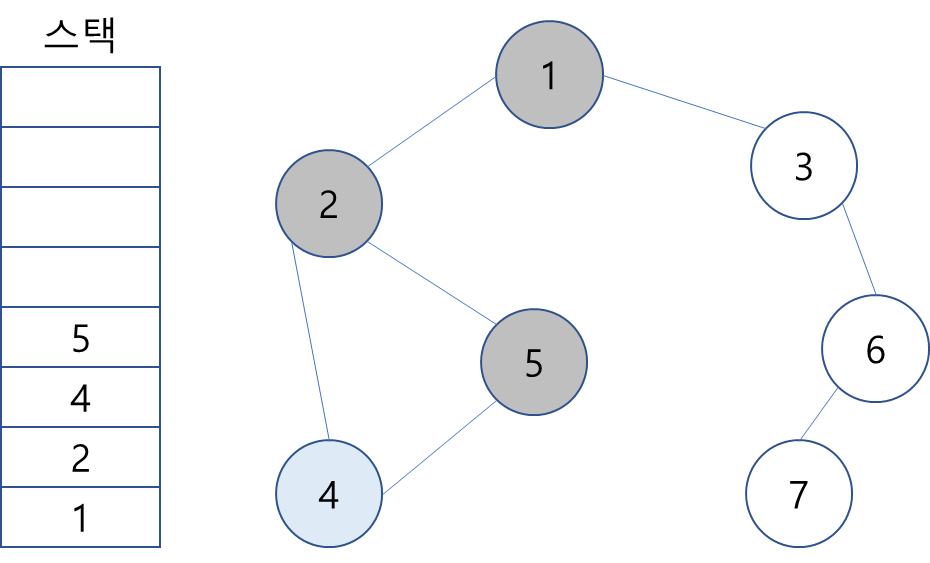
5. 스택 최상단 노드인 5에게는 방문하지 않은 인접 노드가 없기에 없기에 5를 스택에서 제거.
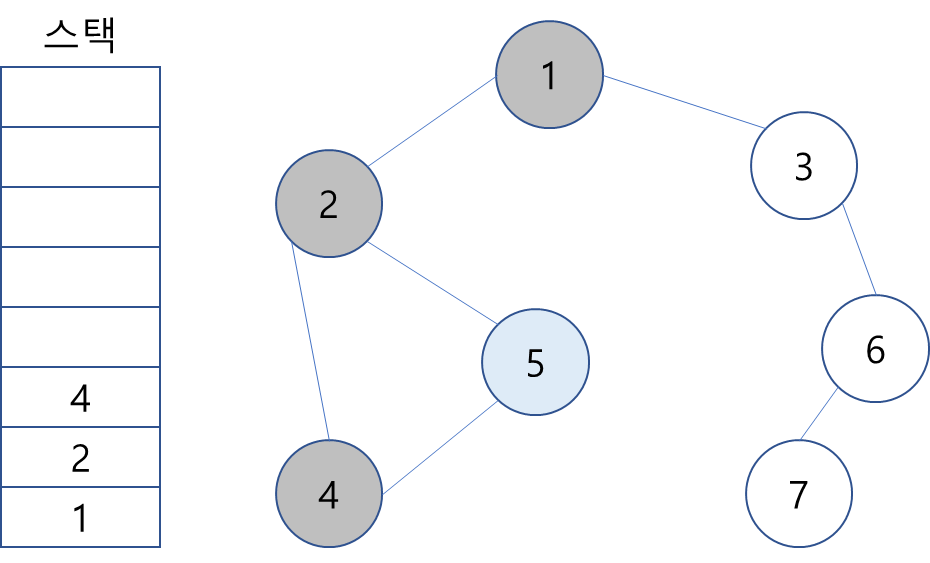
6. 스택 최상단 노드인 4 또한 방문하지 않은 인접 노드가 없기에 스택에서 제거.
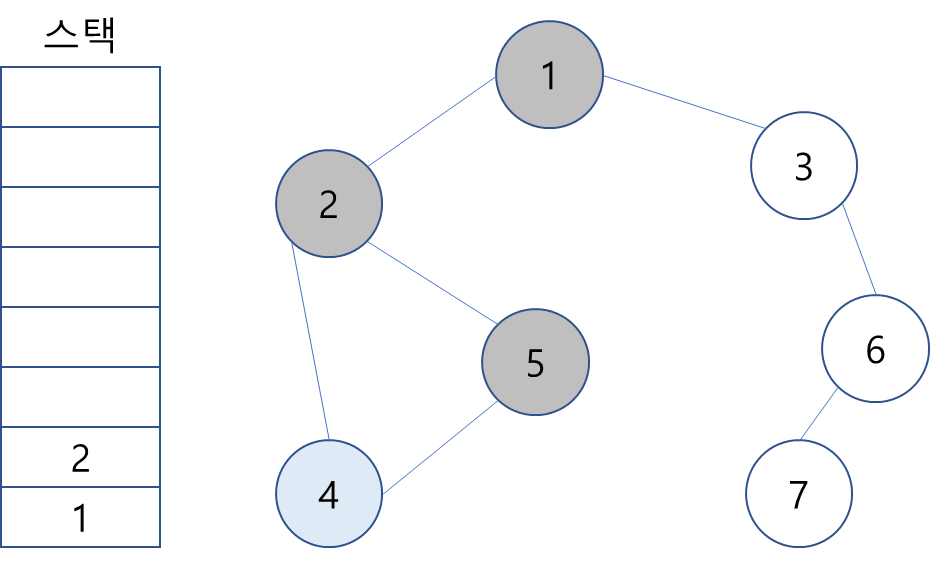
7. 스택 최상단 노드인 2 역시 4와 동일.
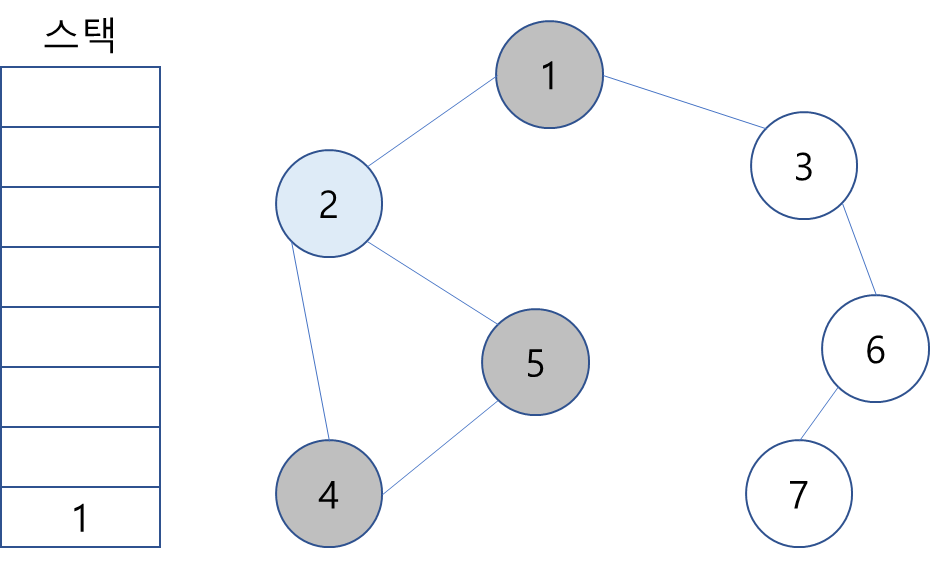
8. 스택의 최상단 노드인 1의 방문하지 않은 인접 노드 3을 스택에 넣고 방문 처리.

9. 스택 최상단 노드 3의 방문하지 않은 인접 노드 6을 스택에 넣고 방문 처리.

10. 스택 최상단 노드인 6의 방문하지 않은 인접 노드 7을 스택에 넣고 방문 처리.
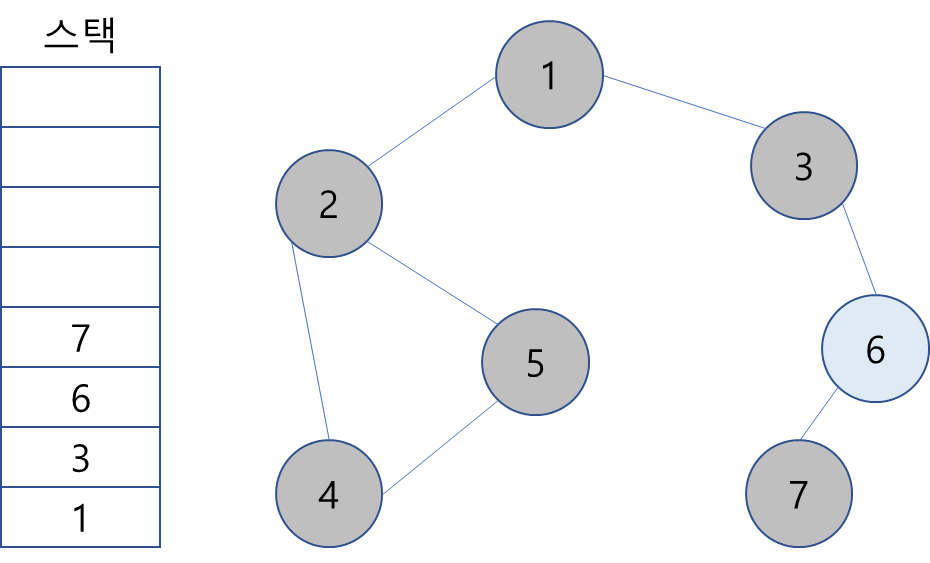
11. 스택 최상단 노드 7은 인접 노드가 없기에 스택에서 제거.
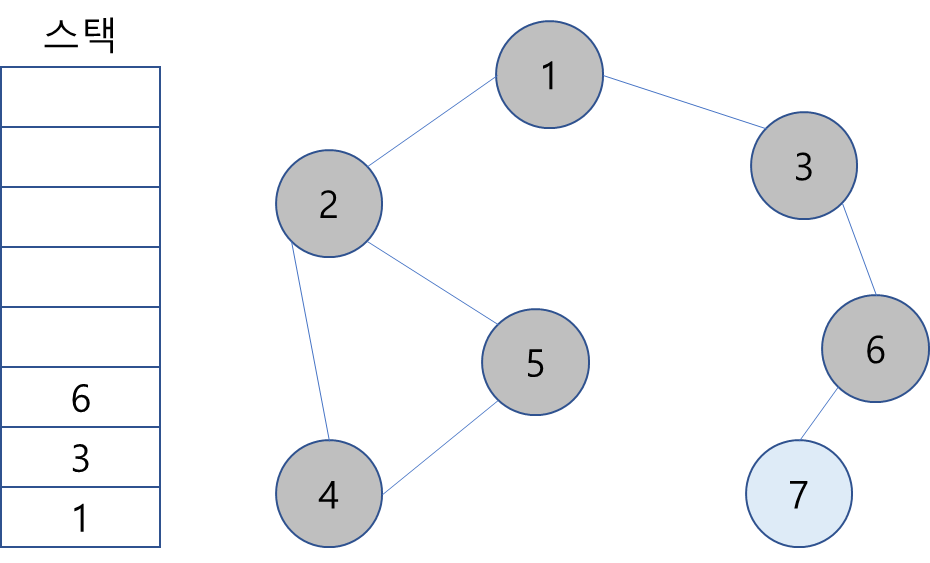
12. 스택 최상단 노드 6은 방문하지 않은 인접 노드가 없기에 스택에서 제거.
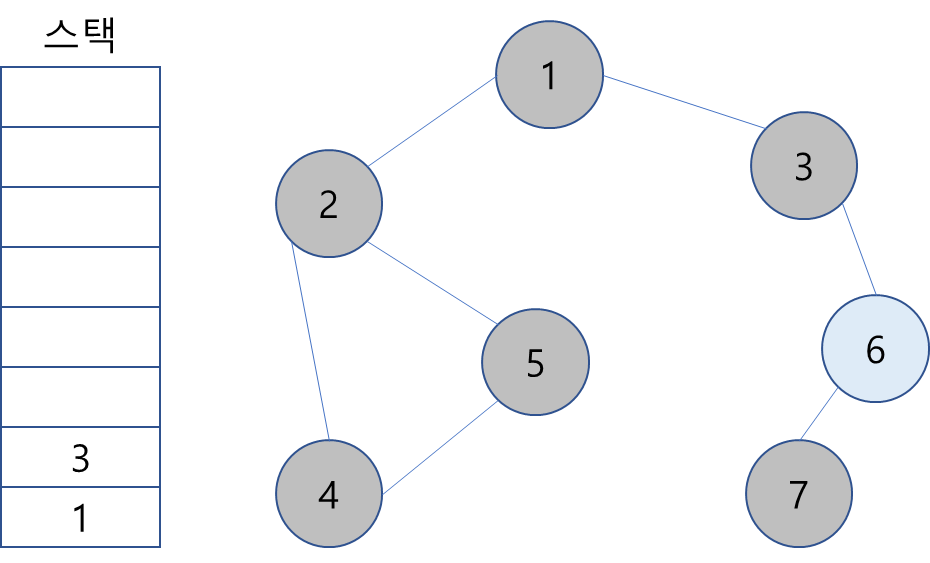
13. 스택 최상단 노드 3도 동일.
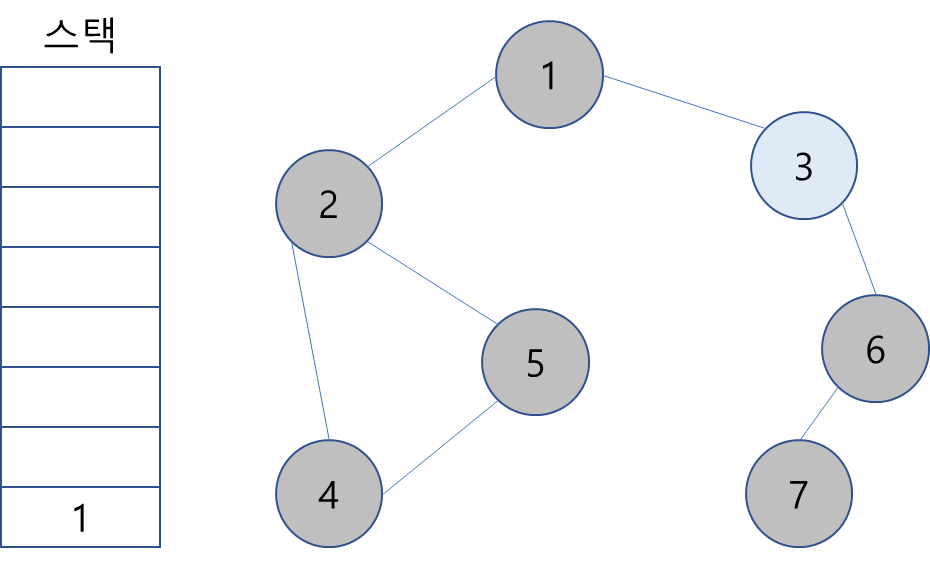
14. 스택 최상단 노드 1도 동일.
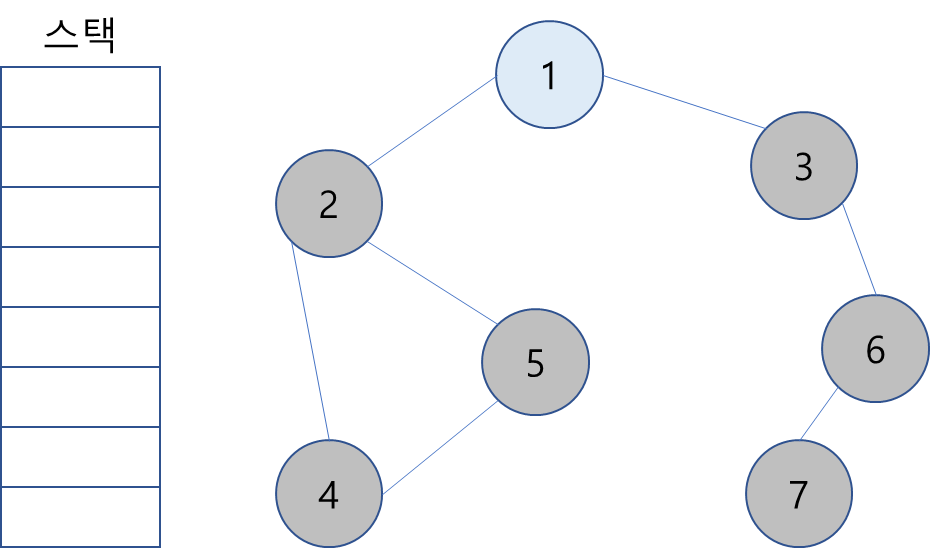
15. 모든 노드를 방문했기에 탐색 종료.
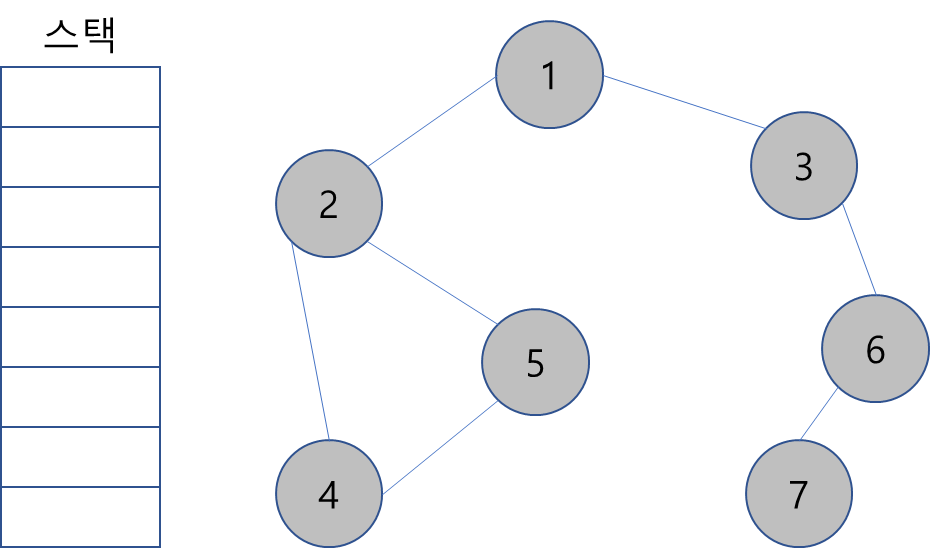
노드의 탐색 순서(스택에 들어간 순서):
1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7
DFS는 구현이 간단하다. 시간 복잡도는 O(N)이며, 재귀 함수로 구현하면 굳이 스택을 사용하지 않아도 되다.
graph = [
[], # 0
[2, 3], # 1
[4, 5], # 2
[6], # 3
[2, 5], # 4
[2, 4], # 5
[3, 7], # 6
[6] # 7
]
# 방문 정보를 기록하기 위한 리스트
visited = [False] * 8
def dfs(v):
# 방문 표시
visited[v] = True
print(v, end=' ')
# 그래프를 순환하면서 인접 노드들을 방문
for i in graph[v]:
# 만약 방문하지 않은 노드가 있다면
if not visited[i]:
# 탐색 시작
dfs(i)
# 탐색 시작 노드 1을 넣어주며 dfs() 실행
dfs(1)
BFS
BFS 너비 우선 탐색이라는 이름에 걸맞게 그래프의 너비부터 탐색한다. DFS가 세로로 탐색하는 반면, BFS는 그래프를 가로로 탐색한다. DFS는 인접 노드의 인접 노드를 계속해서 탐색해 가지만, BFS는 인접 노드를 계속 큐에 넣어가며 큐에 들어온 순서대로 탐색을 시작하기에 시작 노드에서부터 가까운 노드들부터 탐색한다는 의미이다.
구체적인 동작 과정:
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리.
2. 큐에서 노드를 꺼내 해당 노드의 방문하지 않은 모든 인접 노드를 모두 쿠에 삽입하고 방문 처리.
3. 2번 과정을 더 이상 수행할 수 없을 때까지 반복.
DFS와의 차이점을 명확하게 하기 위해 같은 그래프를 탐색하자.

상세한 동작 과정 풀이:
1. 시작 노드인 1을 큐에 삽입하고 방문 처리.
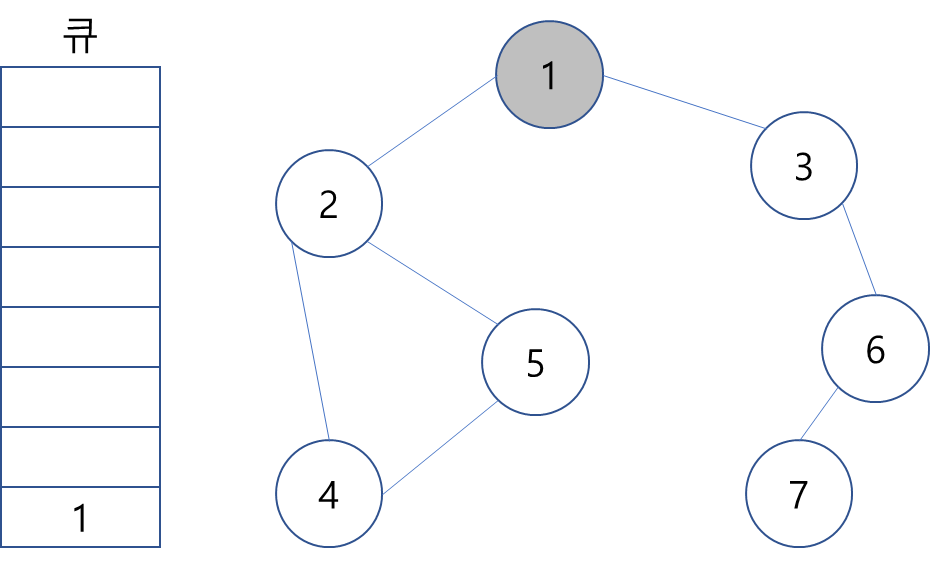
2. 1을 큐에서 꺼내고, 꺼낸 노드의 인접 노드 2와 3을 큐에 삽입하고 방문 처리.
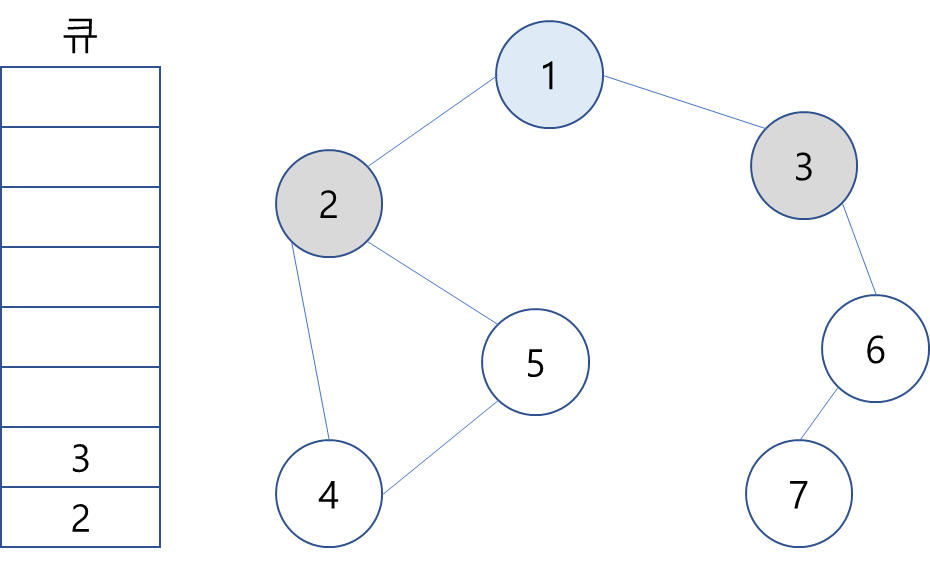
3. 큐에서 2를 꺼내고 방문하지 않은 인접 노드 4와 5를 큐에 삽입하고 방문 처리.
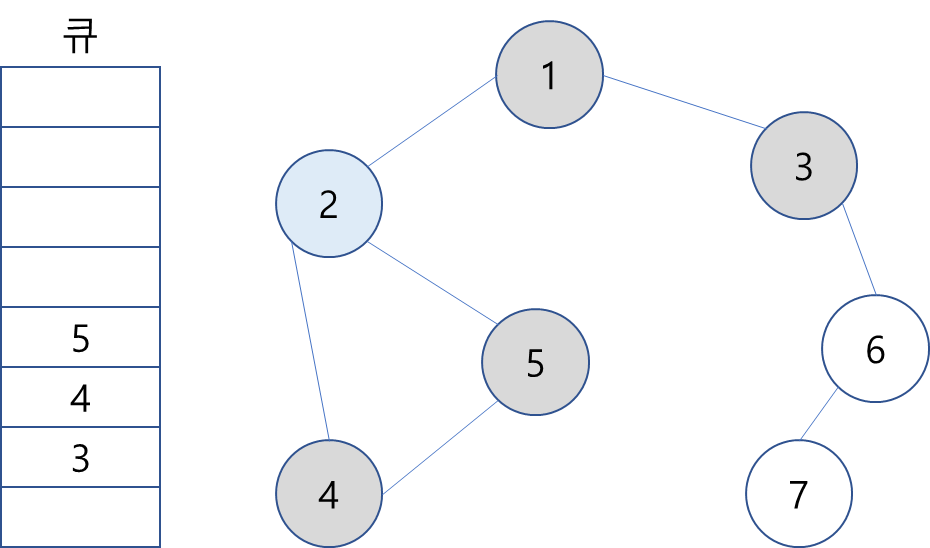
4. 큐에서 3을 꺼내고 방문하지 않은 인접 노드 6을 큐에 삽입하고 방문 처리.

5. 큐에서 4를 꺼내고, 방문하지 않은 인접 노드가 없으므로 무시.
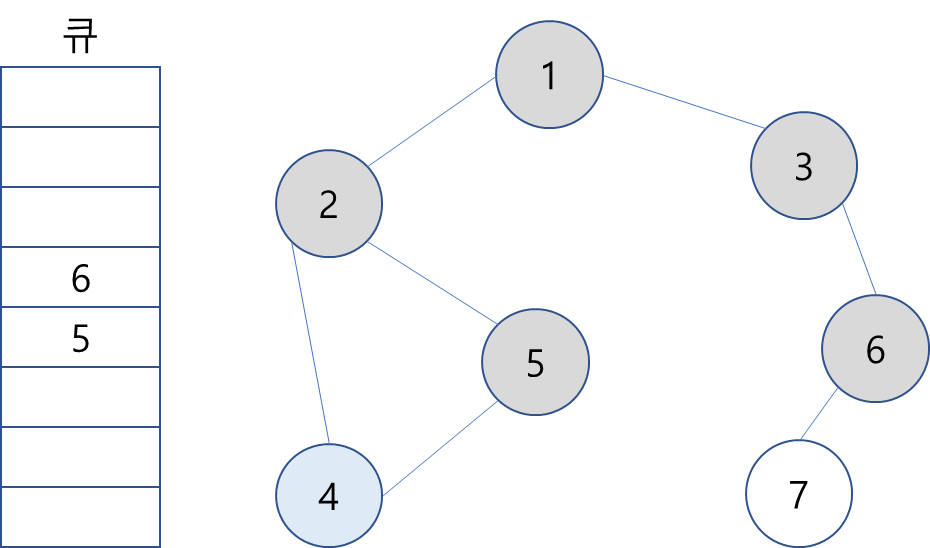
6. 큐에서 5를 꺼내고 방문하지 않은 인접 노드가 없으므로 무시.
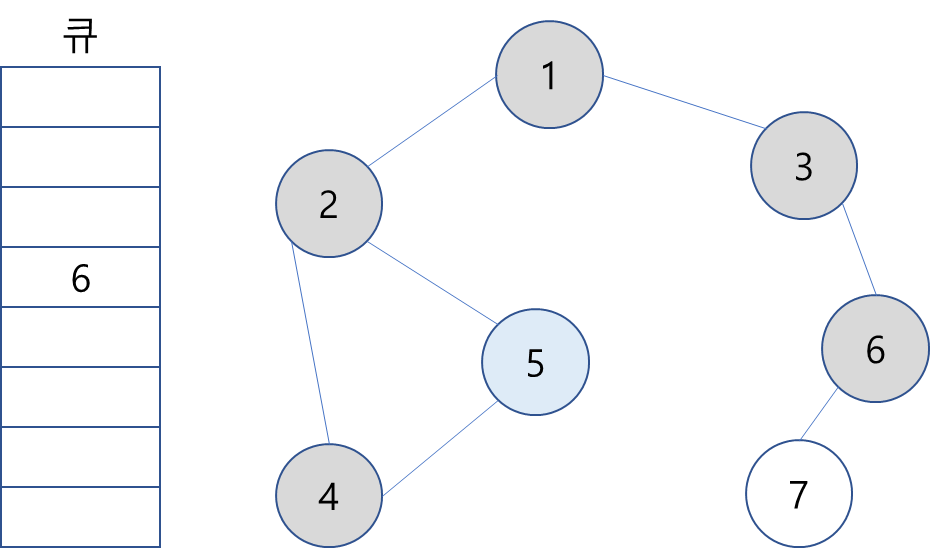
7. 큐에서 6을 꺼내고 방문하지 않은 인접 노드 7을 큐에 삽입하고 방문 처리.
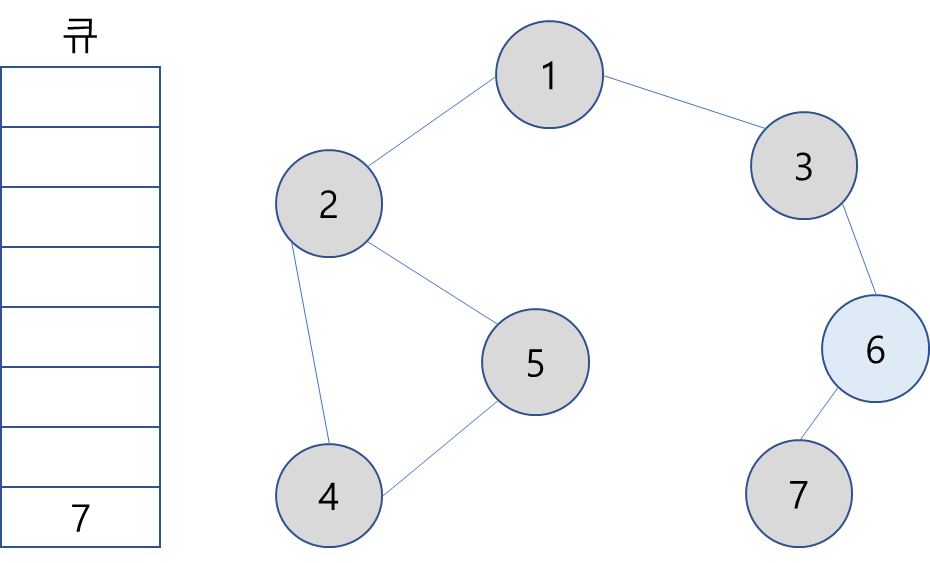
8. 큐에서 7을 꺼내고 방문하지 않은 인접 노드가 없으므로 무시.
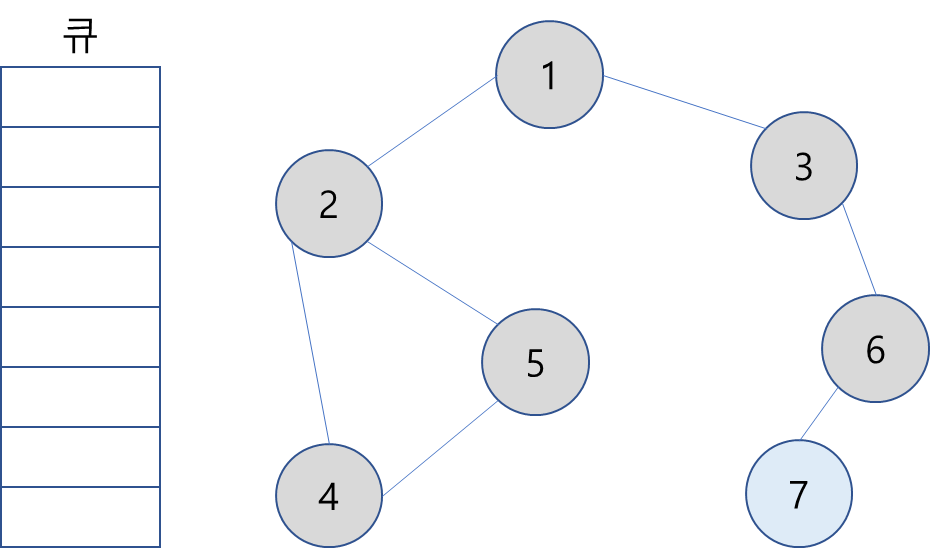
9. 모든 노드를 방문했으므로 종료.
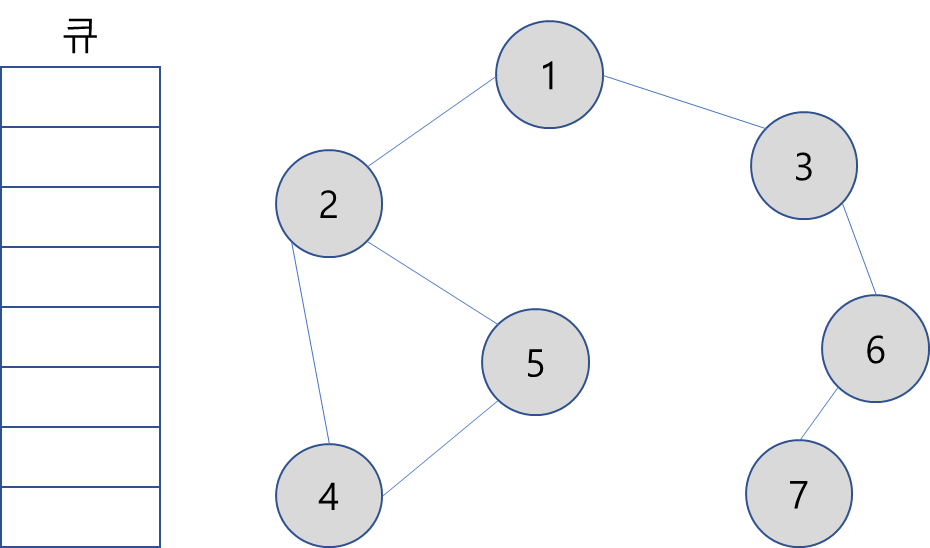
탐색 순서(큐에 들어간 순서):
1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7
BFS는 O(N)의 시간 복잡도를 가지고 있으며 큐를 사용하기에 deque 라이브러리를 사용하는 것을 추천한다. 일반적으로 BFS가 재귀로 구현한 DFS보다 조금 더 빠르게 동작한다.
from collections import deque
graph = [
[], # 0
[2, 3], # 1
[4, 5], # 2
[6], # 3
[2, 5], # 4
[2, 4], # 5
[3, 7], # 6
[6] # 7
]
visited = [False] * 8
def bfs(v):
# 큐 생성 및 큐에 시작 노드 삽입
q = deque()
q.append(v)
# 아직 방문해야 하는 노드가 있다면
while q:
# 큐에서 노드를 꺼내서 x에 저장
x = q.popleft()
print(x, end=' ')
# 그래프를 탐색하다가 방문하지 않은 노드가 있다면
for i in graph[x]:
if not visited[i]:
# 큐에 방문하라고 삽입하고 방문 처리
q.append(i)
visited[i] = True
bfs(1)
응용
이렇게 둘의 차이점을 알아봤는데, 과연 어느 때에 DFS를 사용해야 하며, 어느 때에 BFS를 사용해야 할까? 적절한 사용법을 알기 위해 둘의 장단점을 알아보자.
DFS 장점
- 현 경로상의 노드들만 기억하기 때문에 적은 메모리를 사용. (공간 복잡도)
- 목표 노드가 깊은 단계에 있는 경우 BFS 보다 빠르게 탐색 가능.
DFS 단점
- 해가 없는 경로를 탐색할 경우 단계가 끝날 때까지 (현 경로의 가장 끝까지) 탐색함.
- 답이 아닌 경로가 매우 깊다면, 그 경로에 깊이 빠지게 됨.
- 여러 경로 중 무한한 길이를 가지는 경로가 존재하고 해가 다른 경로에 존재하는 경우, 무한한 길이의 경로에서 빠져나오지 못해 영원히 종료하지 못함
- 효율성을 높이기 위해서 미리 지정한 임의 깊이까지만 탐색하고 (재귀로 구현한다면 재귀 호출 횟수를 제한하는 등), 해를 발견하지 못하면 빠져나와 다른 경로를 탐색하는 방법을 사용해야 함.
- 목표에 이르는 경로가 다수인 경우, DFS는 해에 도착하면 탐색을 종료하기에 얻어진 해가 최단 경로라는 보장이 없음.
BFS 장점
- 모든 경로를 탐색하기에 여러 해가 있을 경우에도 최단 경로임을 보장함.
- 최단 경로가 존재하면 깊이가 무한정 깊어진다고 해도 답을 찾을 수 있음.
- 여러 경로 중 무한한 길이를 가지는 경로가 존재하더라도, 모든 경로를 동시에 탐색을 진행하기 때문에 탐색 가능.
- 노드의 수가 적고, 깊이가 얕은 해가 존재할 때 유리함.
- 탐색하는 트리 또는 그래프의 크기에 비례하는 시간 복잡도를 가짐.
BFS 단점
- 노드의 수가 많을수록 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간(메모리)을 필요로 하게 됨.
- 메모리 상의 확장된 노드들을 저장할 필요가 있기에 탐색하는 트리 또는 그래프의 크기에 비례하는 공간 복잡도를 가짐.
정리하자면 아래와 같이 쓸 수 있다.
| DFS | BFS |
| 스택 또는 재귀 함수 | 큐 |
| 최적 해라는 보장 없음 | 항상 최적 해임을 보장 |
| 그래프 규모가 클 때 | 그래프 규모가 작을 때 |
| 특정 목표 노드를 찾을 때 | 최단 경로를 찾을 때 |
참고:
1. 이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈 저
2. https://covenant.tistory.com/132
DFS BFS란? 백준 문제추천
DFS BFS란? 백준 문제추천 그래프의 모든 노드를 방문 하는 알고리즘으로 DFS와 BFS가 있습니다. 어려운 코딩테스트를 통과하고 나면 만나게 될 기업 기술 면접의 단골 주제입니다. 본 알고리즘에
covenant.tistory.com
3. https://iridescent-zeal.tistory.com/m/25
[알고리즘]그래프 탐색하기: BFS & DFS
그래프의 특정 정점에서 시작하여 나머지 모든 정점을 방문하는 문제를 그래프 순회 문제(graph traversal problem)이라고 합니다. 그래프 순회 문제는 그래프에서 특정 정점을 찾기 위한 용도로 사
iridescent-zeal.tistory.com
4. https://wikidocs.net/123116
0.3.1 DFS와 BFS의 장단점
### 깊이 우선 탐색의 장단점 - 장점: - 최선의 경우, 가장 빠른 알고리즘이다. ‘운 좋게’ 항상 해에 도달하는 올바른 경로를 ...
wikidocs.net
Artificial Intelligence/Search/Exhaustive search/Breadth-first search - Wikibooks, open books for an open world
Breadth-first search (BFS) technique is a systematic search strategy which begins at an initial node (an initial state) and from the initial node search actions are applied downward on a tree structure in a breadth-wise order. The search action consists of
en.wikibooks.org
6. https://namu.wiki/w/%EB%84%88%EB%B9%84%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89
7. https://namu.wiki/w/%EA%B9%8A%EC%9D%B4%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89
'알고리즘 PS > 알고리즘' 카테고리의 다른 글
| [Python] 재귀함수 (2) | 2022.06.12 |
|---|---|
| [Python] 이분/이진 탐색 (0) | 2022.03.02 |
| [Python/C] 반례/테스트 케이스 생성기 만들기 (1) | 2022.02.26 |
| [Python] 그래프 (인접 행렬, 인접 리스트) + DFS/BFS를 배우기 앞서 알아야 할 개념들 (탐색 알고리즘, 자료구조) (0) | 2022.01.30 |
| [Python] 백트래킹 (+ DFS와 차이) (6) | 2022.01.18 |




댓글