이분/이진 탐색이란?
이분 또는 이진 탐색이라 불리는 이 탐색은(이하 이분 탐색) 탐색 범위를 반씩 좁혀가는 탐색하는 알고리즘이다.
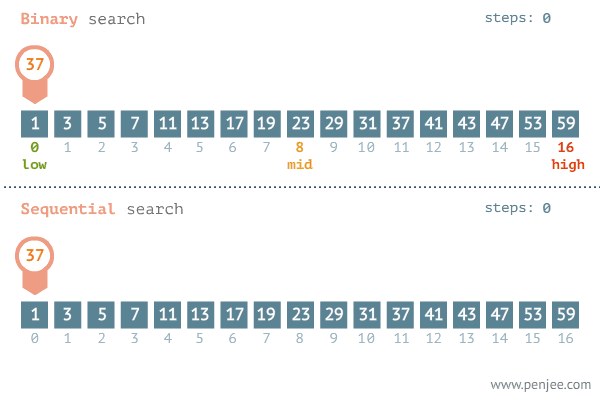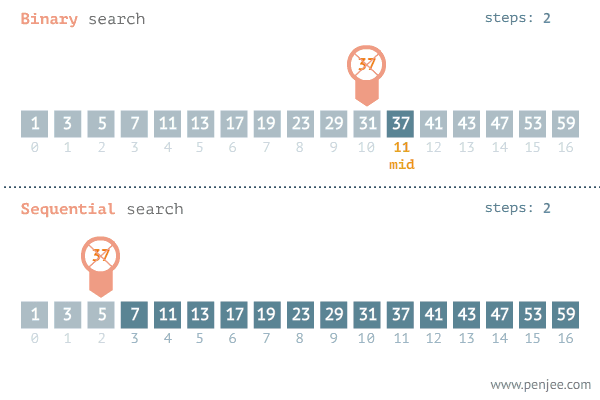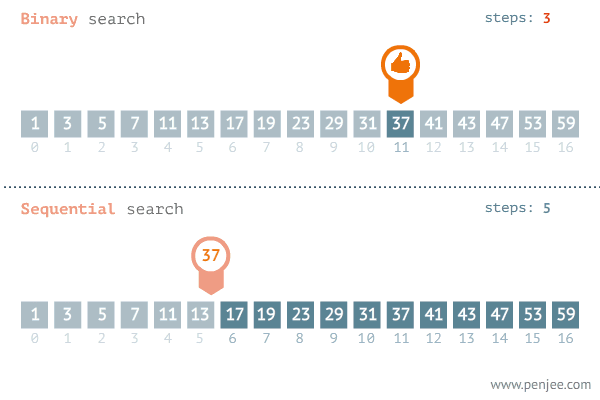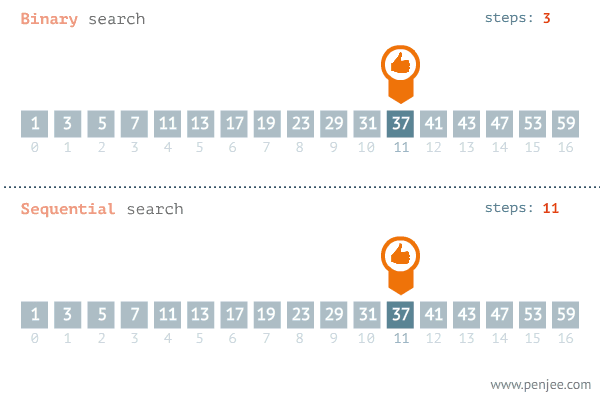
이분 탐색은 결정 문제의 답이 이분적일 때, 그리고 데이터가 정렬되어 있을 때 사용할 수 있다. 보통 정렬되지 않은 리스트를 탐색해야 할 때 앞에서부터 순차적으로 확인하는 탐색인 순차 탐색을 쓰지만, 원소를 하나씩 확인해야 하기에 시간 복잡도가 O(n)이다. 그러나 이분 탐색은 계속해서 탐색 범위를 반으로 줄여나가기에 O(logN)으로 순차 탐색보다 빠르다.
구현
이분 탐색을 구현하는 방법에는 2가지가 있다. 하나는 재귀 함수, 그리고 다른 하나는 반복문을 사용하는 것이다.
재귀 함수로 구현
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
else:
return binary_search(array, target, mid + 1, end)데이터가 들어있는 배열, 찾아야 하는 데이터, 탐색하고 하는 범위의 시작점, 끝점을 요소로 받은 뒤, 배열의 중앙에 있는 데이터 array[mid]와 target을 비교하여 그 값에 따라 리턴 값을 조정하는 방식이다.
만약 array[mid]와 target이 같다면 return, array[mid]가 더 크다면 target이 배열 중앙보다 앞쪽에 있다는 뜻임으로 끝점인 end를 중앙점 바로 앞으로 조정하고 함수 호출, 반대라면 시작점을 중앙점 바로 뒤로 조정하고 함수 호출하는 것이다. 이런 식으로 데이터를 계속 찾다가 못 찾으면 범위를 벗어나게 되고, 함수는 종료하는 것이다.
반복문으로 구현
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
if array[mid] == target:
return mid
elif array[mid] > target:
end = mid - 1
else:
start = mid + 1
return None위의 재귀 함수로 구현한 것과 마찬가지로, while문으로 범위를 벗어나기 이전까지 계속 중앙값과 비교하면 찾다가, 찾으면 그 즉시 return, 없다면 None을 return하는 것이다.
활용
파라메트릭 서치
Parametric Search는 이분 탐색을 활용해서, 최적화 문제(가능한 해 들 중에서 가장 좋은(최소 혹은 최대) 해를 찾는 문제)를 결정 문제(예 또는 아니오로 답하는 문제)로 바꾸어 해결하는 기법이다. 바꾸어 말하자면, 원하는 조건을 만족하는 가장 알맞은 값을 찾을 때, 이 조건을 찾는 과정에서 답이 이분적일 때(예 또는 아니오로 답하기 가능) 파라메트릭 서치를 사용한다.
문제
1654번: 랜선 자르기
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그
www.acmicpc.net
풀이
우선 '원하는 조건을 만족하는 가장 알맞은 값'을 찾아야 한다. 이 문제에선 '이 길이로 자르면 조건을 만족하는 가'를 살펴야 한다.
조건은 N개의 랜선을 만들 수 있는 최대의 길이임으로, 이렇게 단계를 정할 수 있다.
1. 중간점의 길이로 랜선을 잘랐을 때, 생성되는 랜선의 개수를 저장
2. 랜선의 개수가 N개인지 확인
3. N개 미만인지 이상인지 여부에 따라서 시작점과 끝점을 조정
그리하여 이것을 코드로 적으면 이렇게 된다.
K, N = map(int, input().split())
lines = []
for i in range(K):
lines.append(int(input()))
s = 1 # 랜선의 길이가 0일 수가 없기에 최소 값인 1
e = max(lines)
res = 0
while s <= e:
cnt = 0
m = (s+e)//2
for i in lines:
if i >= m: # 만약 랜선의 길이가 m보다 크거나 작다면
cnt += i // m # 몇 개나 잘리는지 저장
if cnt < N:
e = m - 1 # 랜선의 개수가 부족하다면 이 길이가 너무 긴것임으로 끝점을 조정
else:
res = m
s = m + 1 # 최대 길이를 찾아야하기에 길이를 더 늘리기 위해 시작점을 조정
print(res)
맺음말
이분 탐색은 코딩 테스트에서 단골로 잘 나오는 문제다. 여기까지만 보면 쉬워 보이나, off-by-one error나, 시작점이나 끝점을 잘못 선언해서 틀리는 경우 등 실수하기 쉽다. 이런 난관에 봉착했을 때 같이 보면 좋은 글 하나를 남기며 이만 글을 마친다.
같이 보면 좋은 글: 이분 탐색(Binary Search) 헷갈리지 않게 구현하기
참고:
1. 이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나종빈 저
이것이 취업을 위한 코딩 테스트다 with 파이썬 - YES24
나동빈 저자의 유튜브 라이브 방송 https://www.youtube.com/c/dongbinnaIT 취준생이라면 누구나 입사하고 싶은 카카오 · 삼성전자 · 네이버 · 라인!취업의 성공 열쇠는 알고리즘 인터뷰에 있다!IT 취준생
www.yes24.com
2. https://blog.penjee.com/binary-vs-linear-search-animated-gifs/
Binary Vs Linear Search Through Animated Gifs
Average Case Worst Case Binary Search Best Case Binary Search If you're into searching, maybe you're also into sorting! Check out our Sort Detective for exploring common sorting algorithms.
blog.penjee.com
'알고리즘 PS > 알고리즘' 카테고리의 다른 글
| [Python] 재귀함수 (2) | 2022.06.12 |
|---|---|
| [Python] DFS & BFS (0) | 2022.03.19 |
| [Python/C] 반례/테스트 케이스 생성기 만들기 (1) | 2022.02.26 |
| [Python] 그래프 (인접 행렬, 인접 리스트) + DFS/BFS를 배우기 앞서 알아야 할 개념들 (탐색 알고리즘, 자료구조) (0) | 2022.01.30 |
| [Python] 백트래킹 (+ DFS와 차이) (6) | 2022.01.18 |




댓글